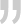
How can we design an efficient active crystal oscillator circuit diagram? First, we need to understand what an active crystal oscillator circuit is? This is the basic knowledge of active crystal oscillators. The active crystal oscillator circuit consists of an amplifier and a feedback network. The feedback network obtains specific outputs from the amplifier and sends them back to the input of the amplifier. It looks quite simple when drawn (as shown in the figure below, amplifier: amplifier, feedback network: feedback network).

But the deeper you go, the more complex it becomes.

To operate a crystal oscillator circuit effectively, two key conditions must be met:

1. The loop power gain must be equal to the homophonic tone

2. The phase shift of the loop must be equivalent to radians such as 0, 2Pi, and 4Pi

The power guided back to the amplifier input must be sufficient to supply the amplifier input, oscillator output, and overcome circuit losses

The precise frequency of an oscillator is determined by the phase shift of the loop within the oscillator circuit. Any change in phase shift will result in a change in frequency. One of the best ways to reduce net phase shift is to use quartz crystals in the feedback loop.

When quartz crystals are used in the feedback loop of an oscillator, the frequency output of the oscillator is actually self regulating. Quartz crystals create a reactance that meets the requirements of the phase loop

Seven key considerations for crystal oscillator circuit design

1. Series circuit

Series circuit crystal oscillators use crystals designed to operate at their natural resonant frequency. This type of circuit does not require capacitance in the feedback loop. Series resonant oscillator circuits are quite basic and are often used due to their small number of components

Series circuits can provide feedback paths other than through crystals. This means that the circuit can continue to oscillate at subjective frequencies Even during crystal failure

A significant drawback of a series circuit is that if the system needs to be modified, you cannot adjust the output frequency. Series resonant crystals are designed according to preferred frequencies, tolerances, and stability, and can be maintained without the need for selective adjustments

2. Load capacitance

Load capacitors can play a crucial role in oscillator circuit design. You will see an example of the importance of load capacitance in the next design consideration, but now let's take a closer look at the load capacitance itself

Load capacitance is described as the amount of capacitance measured or calculated at the crystal terminals in a circuit

When it comes to series circuits, there is no capacitance between the connection points of crystal circuits. Therefore, there is no load capacitor in the circuit. For parallel circuits, the situation is different

To determine the load capacitance in a parallel circuit, use this convenient equation

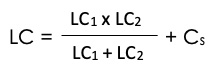
In this equation, LC1 and LC2 represent the load capacitance. Cs is the stray capacitance of a circuit (usually between 3 and 5 pF)

3. Parallel circuit

A parallel resonant circuit is designed using a crystal that operates under a specific load capacitance. This results in the operating frequency of the crystal oscillator being higher than the series resonant frequency but lower than the true parallel resonant frequency

In order to complete the feedback loop of this type of circuit, you must design a path through the crystal. If the crystal fails, the circuit will no longer oscillate

So, where does the "load capacitance" that determines the frequency of the oscillator come from? This circuit actually uses a separate frequency converter with two capacitors in the feedback loop, including the load capacitor. If the load capacitance changes, the frequency generated by the oscillator will also change

At this point, it should be noted that if adjustments are needed, this type of circuit is not suitable for easy frequency adjustment. In addition, precise frequency control and precise load capacitor specifications are required

For example, if a 20 MHz crystal with a capacity of 20 pF is placed in a circuit evaluated as 30 pF, the crystal will be below the specified value. However, if the evaluation value of the circuit is only 10 pF, the frequency will be higher than the specified value

4. Drive power

The driving level refers to the amount of power consumed by a crystal during operation. Power is usually described in milliwatts or microvolts

Quartz crystals are designated as a specific high driving level value that can affect the frequency and operating mode of the oscillator. It is important to collaborate with your crystal oscillator supplier to determine the maximum driving level that the quartz oscillator can withstand

So, what happens if the crystal oscillator exceeds the large driving level? It may cause the oscillator to

1) Becoming unstable

2) Accelerate aging rate

3) Causing communication or timing losses in critical applications

To calculate the driving level of a crystal, please use this formula (basically just Ohm's law, but for power)

Drive Level=(Irms2 x R)

Irms=measured root mean square current through quartz crystal
R=high resistance of quartz crystal

To measure the actual driving level of a crystal oscillator circuit, you can insert a resistor into the crystal circuit. Then the voltage drop on the resistor can be read to calculate current and power dissipation. Of course, make sure to move the resistance away after this measurement

5. Frequency and Mode

The frequency of a crystal oscillator may be limited by its physical size. Sometimes, this may be the length and width of certain applications. At other times, it may be the thickness of the quartz crystal itself. The thinner the quartz wafer, the higher the frequency. The thickness of quartz wafers usually becomes too thin to handle around 30MHz

If you need an oscillator with a frequency higher than the limit frequency, you can use the "fundamental frequency". The fundamental frequency is the low frequency generated by the overall oscillation of an object, which is different from higher frequency harmonics. If the fundamental frequency of a crystal is 10 megahertz, it can also oscillate at fundamental frequencies of 3, 5, 7, etc. Therefore, the oscillator can oscillate at frequencies such as 30MHz, 50MHz, 70MHz, etc. These are all overtones at that frequency

When using overtone frequencies, crystal manufacturers must design the crystal to operate at the desired overtone frequency. Do not attempt to order a crystal with one fundamental mode and then operate with another desired overtone, as the manufacturing process of fundamental and overtone crystals is different

6. Design considerations

To achieve optimal oscillator circuit operation, some design considerations should be followed. It has always been recommended to avoid using parallel lines in circuits. This can reduce stray capacitance. All lines should be as short as possible to prevent coupling. Maintaining component isolation by using a ground plane can also be helpful

7. Negative resistance

The design of oscillators must strengthen negative resistance to achieve optimal performance. Negative resistance is often referred to as "oscillation allowance"

Here are 6 simple steps to help you calculate the negative resistance in the oscillator circuit

1) Temporarily connect a variable resistor in series with the crystal

2) Set the resistance to a low setting (close to zero ohms)

3) Power on the oscillator and monitor the output on the oscilloscope

4) When you continuously monitor the oscilloscope signal, start using variable resistors to increase the resistance in the circuit

5) Once the oscillation stops, record the variable resistance to determine the ohmic value

6) Add the high resistance value of the crystal (specified by the supplier) to the ohmic value measured in step 5

The calculated total value is called "negative resistance" or "oscillation margin". As a general rule of thumb, negative resistance should be at least 5 times the specified high resistance value of the crystal to be reliable.

The above is a suggestion from our Blue Wood team on the design of active crystal oscillator circuits. We hope that everyone can avoid detours in designing oscillator circuits and complete the circuit design of crystal oscillator products more quickly to match the products.